Um dado ponto em uma corda por onde passa uma onda senoidal apresenta menor velocidade quando
o módulo do deslocamento é máximo
o módulo da aceleração é máximo
o módulo do deslocamento é mínimo
o módulo do deslocamento é metade da amplitude
o módulo do deslocamento é um quarto da amplitude
Passo 1
Sabemos que a velocidade é derivada da posição e isso vale para a velocidade transversal de uma onda em corda. Temos que
Ao analisarmos o gráfico da posição de uma onda na corda
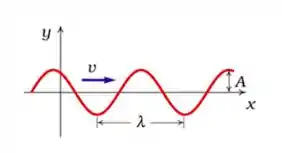
Vemos que onde tiver máxima amplitude (deslocamento) teremos derivada igual a zero. Assim, velocidade nula.
Portanto teremos menor velocidade, quando tivermos o máximo deslocamento.
Resposta
Alternativa
Exercícios de Livros Relacionados
13.1. A corda de um piano emite um lá médio vibrando com uma frequência primaria igual a 220 Hz. a) Calcule o período e a frequência angular. b) Calcule a frequência angular de uma soprano emitindo um
Feixes de laser enviados para a Lua são um recurso rotineiro para se determinar com precisão a distância entre a Terra e a Lua. No entanto, para determinar a distancia com precisão, correções devem se
Use a equação de onda para determinar a velocidade de uma onda dada por y x , t = 3,00m m sen [ 4,00m - 1 x - 7,00s - 1 t ] .
Se, no exemplo 15.3 você não desprezasse a massa da corda, qual seria a velocidade da ondaNa extremidade inferior da corda;No meio da corda;Na extremidade superior da corda?
Um oscilador harmônico simples em x = 0 gera uma onda em uma corda. O oscilador opera em uma frequência de 40 H z e com uma amplitude de 3 c m . A corda possui uma densidade linear de 50 g / c m e est